Introduction
In the previous chapter it was shown that exact mathematical situations for the forces exerted by fluids at rest could be readily obtained. This is because in hydrostatic only simple pressure forces are involved. When a fluid in motion is considered, the problem of analysis at once becomes much more difficult. Not only have the particle velocity's magnitude and direction to be taken into account, but there is also the complex influence of viscosity causing a shear or frictional stress between the moving fluid particles and at the containing boundaries. The relative motion which is possible between different elements of the fluid body causes the pressure and shear stress to vary considerably from one point to another according to flow conditions. Owing to the complexities associated with the flow phenomenon, a precise mathematical analysis is only possible in a few, and from the engineering point of view, some what impractical,cases.It is therefore necessary to solve flow problems either by experimentation, or by making certain simplifying assumptions sufficient to obtain a theoretical solution. The two approaches are not mutually exclusive, since the fundamental laws of mechanics are always valid and enable partially theoretical methods to be adopted in several important cases. Also it is important to ascertain experimentally the extent of the deviation from the true conditions consequent upon a simplified analysis.
The most common simplifying assumption is that the fluid is ideal or perfect, thus eliminating the complicating viscous effects. This is the basis of classical hydrodynamics, a branch of applied mathematics that has received attention from such eminent scholars as Stokes, Rayleigh, Rankine, Kelvin and Lamb. There are serious inherent limitations in the classical theory, but as water has a relatively low viscosity, it behaves as a real fluid in many situations. For this reason, classical hydrodynamics may be regarded as a most valuable background to the study of the characteristics of fluid motion. The present chapter is concerned with the fundamental dynamics of fluid motion and serves as a basic introduction to succeeding chapters dealing with the more specific problems encountered in civil engineering hydraulics. The three important basic equations of fluid motion namely, the continuity,Bernoulli, and momentum equations are derived and their significance explained. Later, the limitations of the classical theory are considered and the behaviour of a real fluid described.An incompressible fluid is assumed throughout.
Types of flow
The various types of fluid motion may be classified as follows:
1.Turbulent and laminar
2.Rotational and irrotational
3.Steady and unsteady
4.Uniform and non-uniform.
MVS series axial-flow pumps AVS series mixed-flow pumps (Vertical Axial flow and Mixed flow submersible sewage pump) are modern productions successfully designed by the means of adopting foreign modern technology. The new pumps' capacity are 20%larger than the old ones. The efficiency is 3~5% higher than the old ones.

Turbulent and laminar flow.
These terms describe the physical nature of the flow.
In turbulent flow, the progression of the fluid particles is irregular and there is a seemingly haphazard interchange of position.Individual particles are subject to fluctuating trans. verse velocities so that the motion is eddying and sinuous rather than rectilinear. If dye is injected at a certain point, it will rapidly diffuse throughout the flow stream. In the case of turbulent flow in a pipe,for example,an instantaneous recording of the velocity at a section would reveal an approximate distribution as shown in Figure 1(a). The steady velocity, as would be recorded by normal measuring instruments, is indicated in dotted outline, and it is apparent that turbulent flow is characterised by an unsteady fluctuating velocity superimposed on a temporal steady mean.
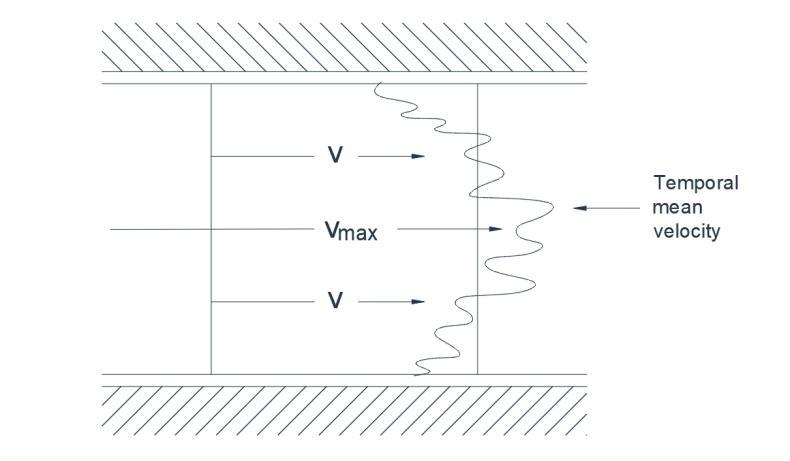
Fig.1(a) Turbulent flow
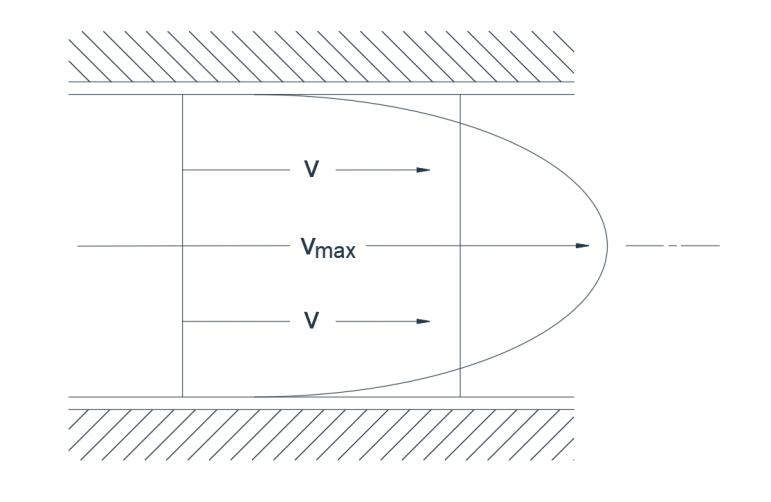
Fig.1(b) Laminar flow
In laminar flow all the fluid particles proceed along parallel paths and there is no transverse component of velocity. The orderly progression is such that each particle follows exactly the path of the particle preceding it without any deviation. Thus a thin filament of dye will remain as such without diffusion. There is a much greater transverse velocity gradient in laminar flow(Fig.1b) than in turbulent flow.For example,for a pipe, the ratio of the mean velocity V and the maximum velocity V max is 0,5 with turbulent flow and 0,05 with laminar flow.
Laminar flow is associated with low velocities and viscous sluggish fluids.In pipeline and open-channel hydraulics, the velocities are nearly always sufficiently high to ensure turbudent flow,although a thin laminar layer persists in proximity to a solid boundary. The laws of laminar flow are fully understood, and for simple boundary conditions the velocity distribution can be analysed mathematically. Due to its irregular pulsating nature, turbulent flow has defied rigorous mathematical treatment, and for the solution of practical problems,it is necessary to rely largely on empirical or semiempirical relationships.

Model No:XBC-VTP
XBC-VTP Series vertical long shaft fire fighting pumps are series of single stage, multistage diffusers pumps, manufactured in accordance with the latest National Standard GB6245-2006. We also improved the design with the reference of the standard of United States Fire Protection Association. It is mainly used for fire water supply in petrochemical, natural gas, power plant, cotton textile, wharf, aviation, warehousing, high-rising building and other industries. It can also apply to ship, sea tank, fire ship and other supply occasions.
Rotational and irrotational flow.
The flow is said to be rotational if each fluid particle has an angular velocity about its own mass centre.
Figure 2a shows a typical velocity distribution associated with turbulent flow past a straight boundary. Due to the non-uniform velocity distribution, a particle with its two axes originally perpendicular suffers deformation with a small degree of rotation.In Figure 2a,flow in a circular
path is depicted, with the velocity directly proportional to the radius. The two axes of the particle rotate in the same direction so that the flow is again rotational.
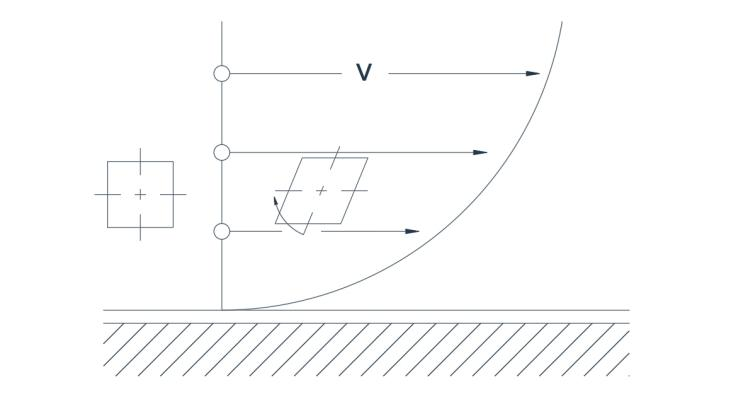
Fig.2(a) Rotational flow
For the flow to be irrotational, the velocity distribution adjacent to the straight boundary must be uniform(Fig.2b). In the case of flow in a circular path, it may be shown that irrotational flow will only pertain provided that the velocity is inversely proportional to the radius. From a first glance at Figure 3, this appears erroneous, but a closer examination reveals that the two axes rotate in opposite directions so that there is a compensating effect producing an average orientation of the axes which is unchanged from the initial state.
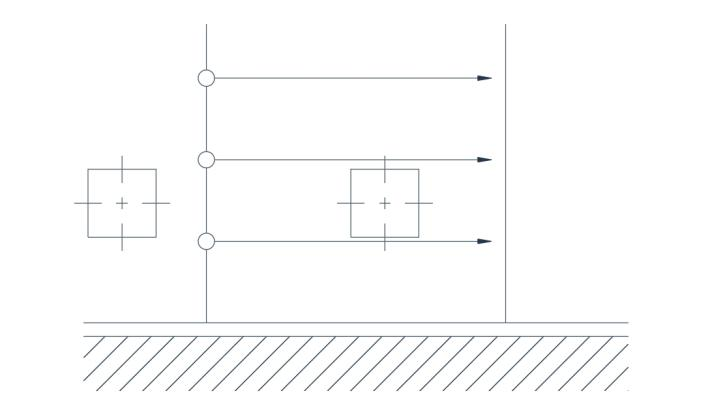
Fig.2(b) Irrotational flow
Because all fluids possess viscosity, the low of a real fluid is never truly irrotation, and laminar flow is of course highly rotational. Thus irrotational flow is a hypothetical condition which would be of academic interest-only were it not for the fact that in many instances of turbulent flow the rotational characteristics are so insignificant that they may be neglected. This is convenient because it is possible to analyse irrotational flow by means of the mathematical concepts of classical hydrodynamics referred to earlier.
Centrifugal Sea Water Destination Pump
Model No:ASN ASNV
Model ASN and ASNV pumps are single-stage double suction split volute casing centrifugal pumps and used or liquid transportation for water works, air-conditioning circulation, building, irrigation, drainage pump station, electric power station, industrial water supply system, fire-fighting system, ship, building and so on.

Steady and unsteady flow.
The flow is said to be steady when the conditions at any point are constant with respect to time. A strict interpretation of this definition would lead to the conclusion that turbulent flow was never truly steady. However, for the present purpose it is convenient to regard the general fluid motion as the criterion and the erratic fluctuations associated with the turbulence as only a secondary influence. An obvious example of steady flow is a constant discharge in a conduit or open channel.
As a corollary it follows that the flow is unsteady when conditions vary with respect to time. An example of unsteady flow is a varying discharge in a conduit or open channel; this is usually a transient phenomenon being successive to, or followed by, a steady discharge. Other familiar
examples of a more periodic nature are wave motion and the cyclic movement of large bodies of water in tidal flow.
Most of the practical problems in hydraulic engineering are concerned with steady flow. This is fortunate, since the time variable in unsteady flow considerably complicates the analysis. Accordingly,in this chapter, consideration of unsteady flow will be restricted to a few relatively simple cases. It is important to bear in mind, however, that several common instances of unsteady flow may be reduced to the steady state by virtue of the principle of relative motion.
Thus,a problem involving a vessel moving through still water may be rephrased so that the vessel is stationary and the water is in motion; the only criterion for similarity of fluid behaviouris that the relative velocity shall be the same. Again, wave motion in deep water may be reduced to the
steady state by assuming that an observer travels with the waves at the same velocity.

Diesel engine Vertical Turbine multistage centrifugal inline shaft water Drainage Pump This kind of vertical drainage pump is mainly used for pumping no corrosion, temperature less than 60 °C, suspended solids (not including fiber, the grits) less than 150 mg/L content of the sewage or waste water. VTP type vertical drainage pump is in VTP type vertical water pumps, and on the basis of the increase and the collar, set the tube oil lubrication is water. Can smoke temperature below 60 °C, send to contain a certain solid grain (such as scrap iron and fine sand, coal, etc.) of sewage or waste water.
Uniform and non-uniform flow.
The flow is said to be uniform when there is no variation in the magnitude and direction of the velocity vector from one point to another along the path of flow. For compliance with this definition, both the area of flow and the velocity must be the same at every cross-ection. Non-uniform flow occurs when the velocity vector varies with the location, a typical example being flow between converging or diverging boundaries.
Both of these alternative conditions of flow are common in open-channel hydraulics, although strictly speaking, since uniform flow is always approached asymptotically, it is an ideal state which is only approximated to and never actually attained. It should be noted that the conditions relate to space rather than time and therefore in cases of enclosed flow(eg.pipes under pressure), they are quite independent of the steady or unsteady nature of the flow.
Post time: Mar-29-2024

